Welcome to the Capacitor Fundamentals Series, where we teach you about the ins and outs of chips capacitors – their properties, product classifications, test standards, and use cases – in order to help you make informed decisions about the right capacitors for your specific applications. After describing soldering for capacitors in our previous article, let’s discuss common formulas and calculations for capacitors.
Dissipation Factor and Capacitive Reactance
When it comes to practical applications, a real-world capacitor is not perfect, such that the voltage and current across it will not be perfectly 90 degrees out of phase. The angle by which the current is out of phase from ideal can be determined (as seen in Figure 1), and the tangent of this angle is defined as loss tangent or dissipation factor (DF).
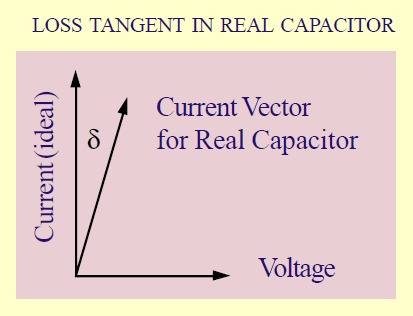
Figure 1. Loss tangent in a real-world capacitor
DF is a material property and is not dependent on geometry of a capacitor. DF greatly influences the usefulness of a dielectric in electronic applications. In practice, it is found that lower DF is associated with materials of lower dielectric constant K. Higher K materials, which develop this property by virtue of high polarization mechanisms, display higher dissipation factor. Dissipation factor and quality (Q) are reciprocals of each other and measure the losses with the capacitor.
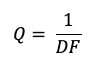
where Q is quality factor and DF is dissipation factor.
Because a capacitor is made of two (or more) conductors separated from each other by an insulator, capacitive reactance is a measure of a capacitor’s opposition to change in voltage or AC voltage flow.
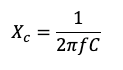where is Xc is capacitive reactance in ohms, f is frequency in hertz and C is capacitance in farads.
Equivalent Series Resistance
Equivalent series resistance (ESR) is a measurement of all the nonideal electrical resistances in series with the capacitor, such as the resistance of the conductor plates, insulating material, terminations, and so forth. The higher the ESR, the more losses occur in the capacitor.
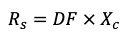
where Rs is ESR in ohms, DF is dissipation factor, and Xc is capacitive reactance in ohms.
ESR also determines how much ripple current is converted into heat generation. High temperatures can adversely affect performance or unexpectedly damage the capacitor in the long run if power dissipation is not properly handled.
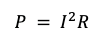
where P is power dissipation in watts, I is root mean square (RMS) current in amps, and R is ESR in ohms.
Hopefully, you know have a better understanding of useful formulas and calculations for capacitors and how they may affect your specific application. This article concludes our 14-part capacitor fundamentals series. For more information, check out our Knowles Precision Devices Capacitors to view our complete product offering and contact us to find out how we can best help you.
To learn more about capacitors, download our ebook, A Guide to Selecting the Right Capacitor for Your Specific Application.
