To help customers with filter selection, we generally provide a lot of information on what our filters can do. But in this new Filter Basics Series, we are taking a step back to cover some background information on how filters do what they do. Regardless of the technology behind the filter, there are several key concepts that all filters share that we will dive into throughout this series. By providing this detailed fundamental filter information, we hope to help you simplify your future filtering decisions.
In part 2, we cover how RF designers can use the different frequency dependencies of capacitors and inductors to manipulate impedance and create various filter responses. 
At the most basic level, filters are necessary in RF devices so that unwanted frequencies do not pass through the circuit and cause interreference. While filtering can become quite complex as operating frequencies increase, it can be made much less daunting by having an understanding of how basic filters are built using standard electrical components such as resistors (Rs), capacitors (Cs), and inductors (Ls).
Before we jump into types of filters though, let’s start by looking at how a voltage divider functions. A voltage divider is a passive linear circuit that produces an output voltage (Vo) that is a fraction of the input voltage (Vi). As shown in Figure 1, the voltage divider changes the Vi down to the Vo based on the values of the resistors used, which are R1 and R2 below.
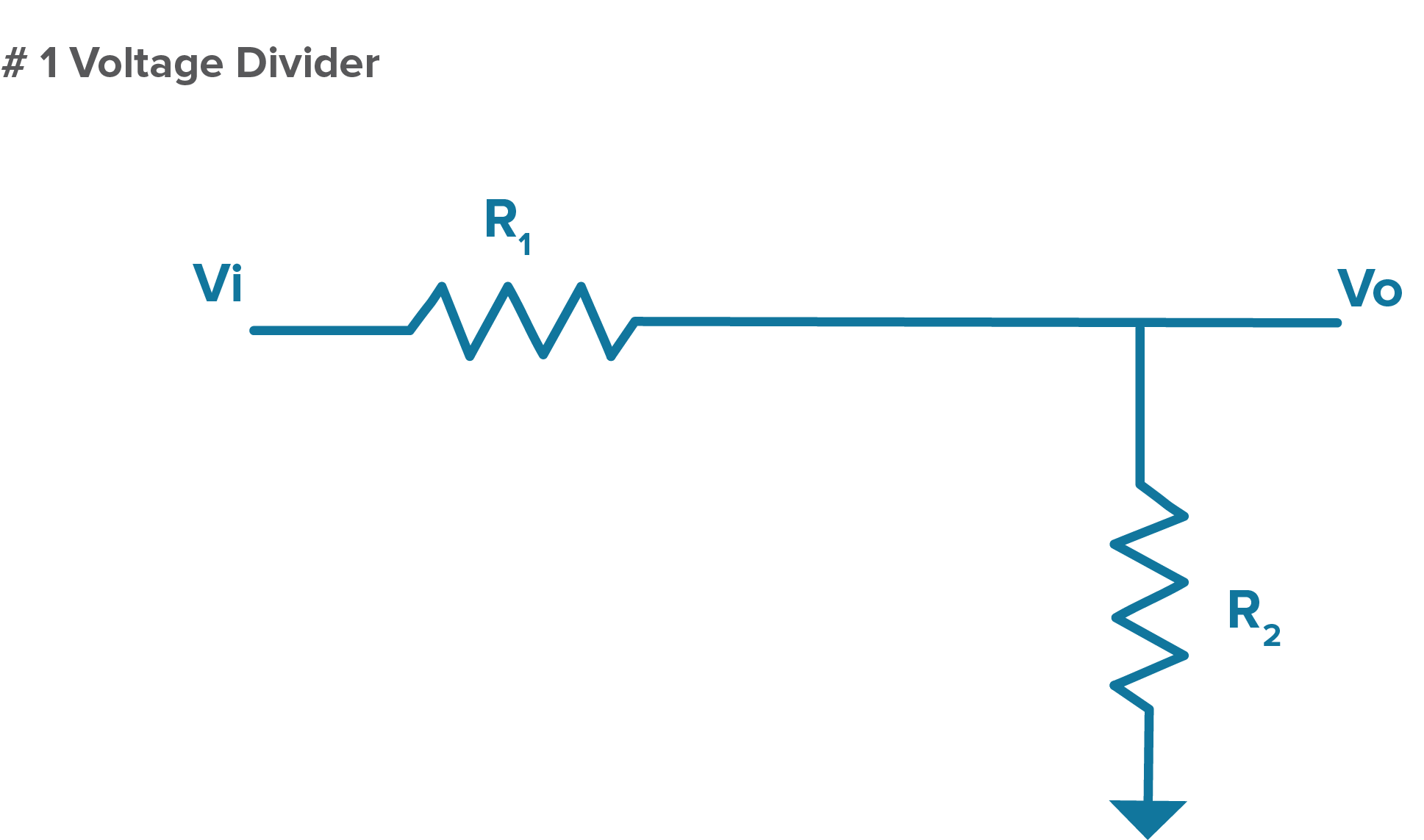
Figure 1. An illustration of the very familiar DC circuit, the voltage divider.
If we start with Ohms Law, which as a reminder, states that electric current is proportional to voltage and inversely proportional to resistance since resistance hinders the flow of current in the circuit, we can derive the following formula for how a voltage divider works:
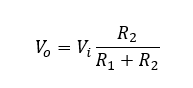
As you can see from the formula above, as R1 grows (or as R2 shrinks) the output voltage will drop.
Swapping Rs and Cs to Turn Our Voltage Divider into a Filter
Now that we know how our simple voltage divider works, let’s look at what happens if we trade out some Rs for Cs. To understand how this works, think back to Part 1 of our series where we covered the fact that inductors and capacitors will act like resistors for AC signals at a certain frequency. Also, in this section we discussed how the impedance of a capacitor will change with frequency and that capacitance can be calculated as follows:
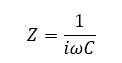
Z = Impedance, Omega = Angular Frequency, i is the imaginary number since we are using complex numbers here, and C = Capacitance.
Thus, for a capacitor, impedance decreases with frequency. So, if we swap R2 for a C as shown in Figure 2, we will have a low-pass RC filter, which is a filter circuit that passes frequency signals below a certain cutoff frequency and blocks frequency signals higher than that point.
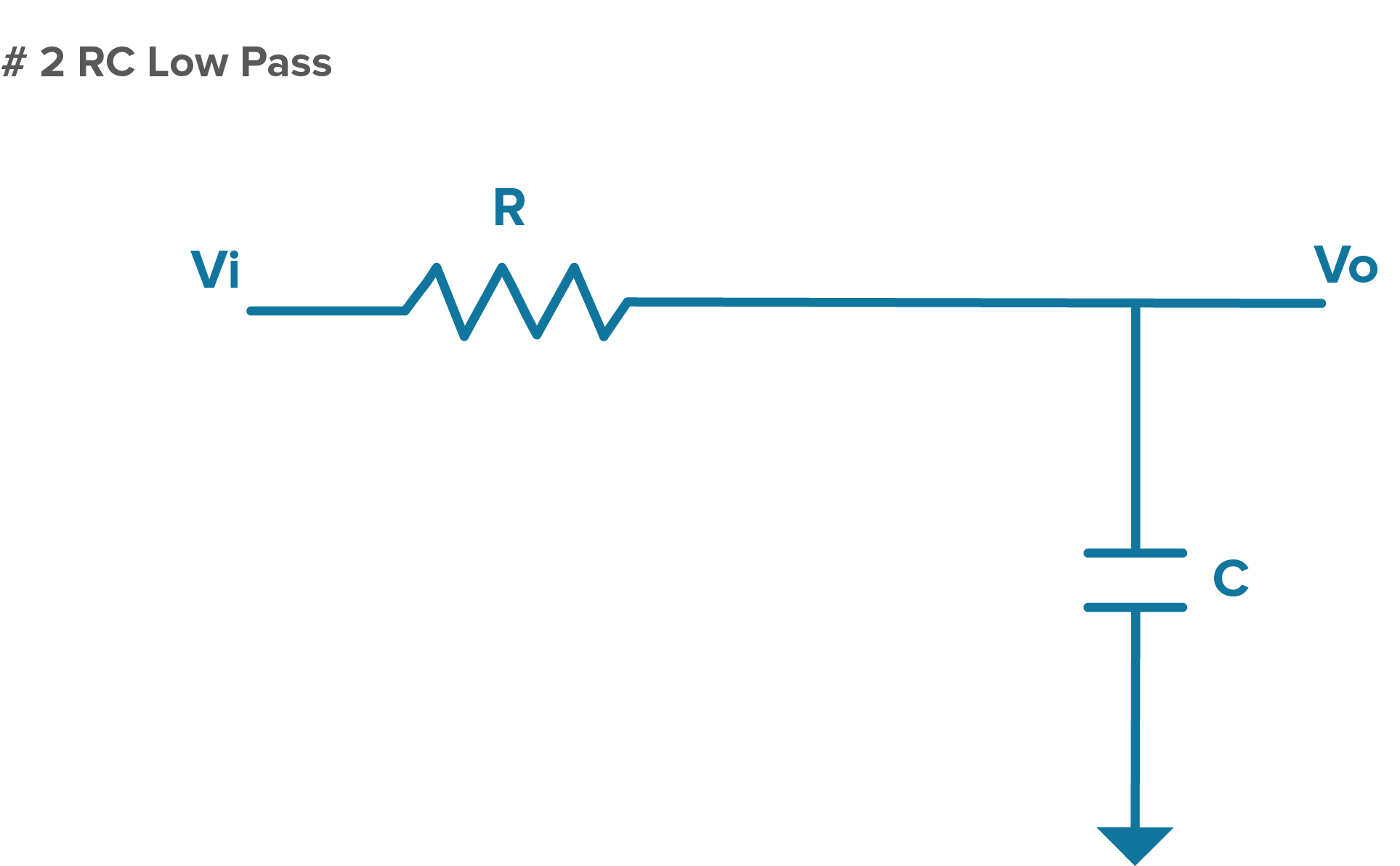
Figure 2. A diagram of an RC low-pass filter.
In the RC low-pass filter, the path to ground goes through a capacitor, which means impedance will decrease with increasing frequency. Therefore, in this circuit, the ratio of the Vi down to the Vo will depend on the values of R and C and the frequency of the signal. With high frequencies, impedance is low and energy is sent to ground as Vi is divided down. Low frequencies see a higher impedance and energy is sent to the output.
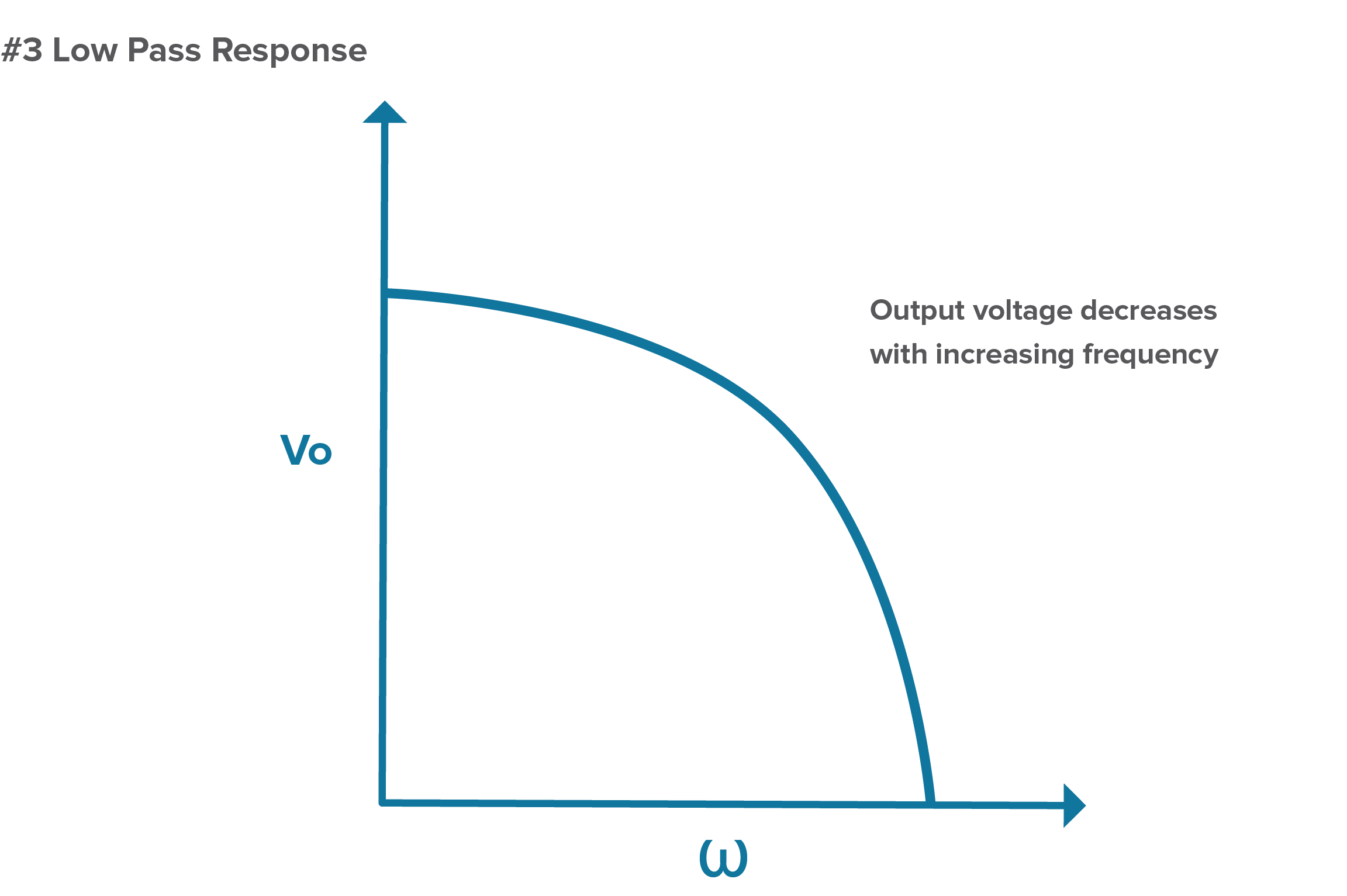
Figure 3. Output voltage decreases with increasing frequency in an RC low-pass filter.
If we do this the other way around and replace R1 with a C, the path to output goes through the capacitor and we get the opposite effect.
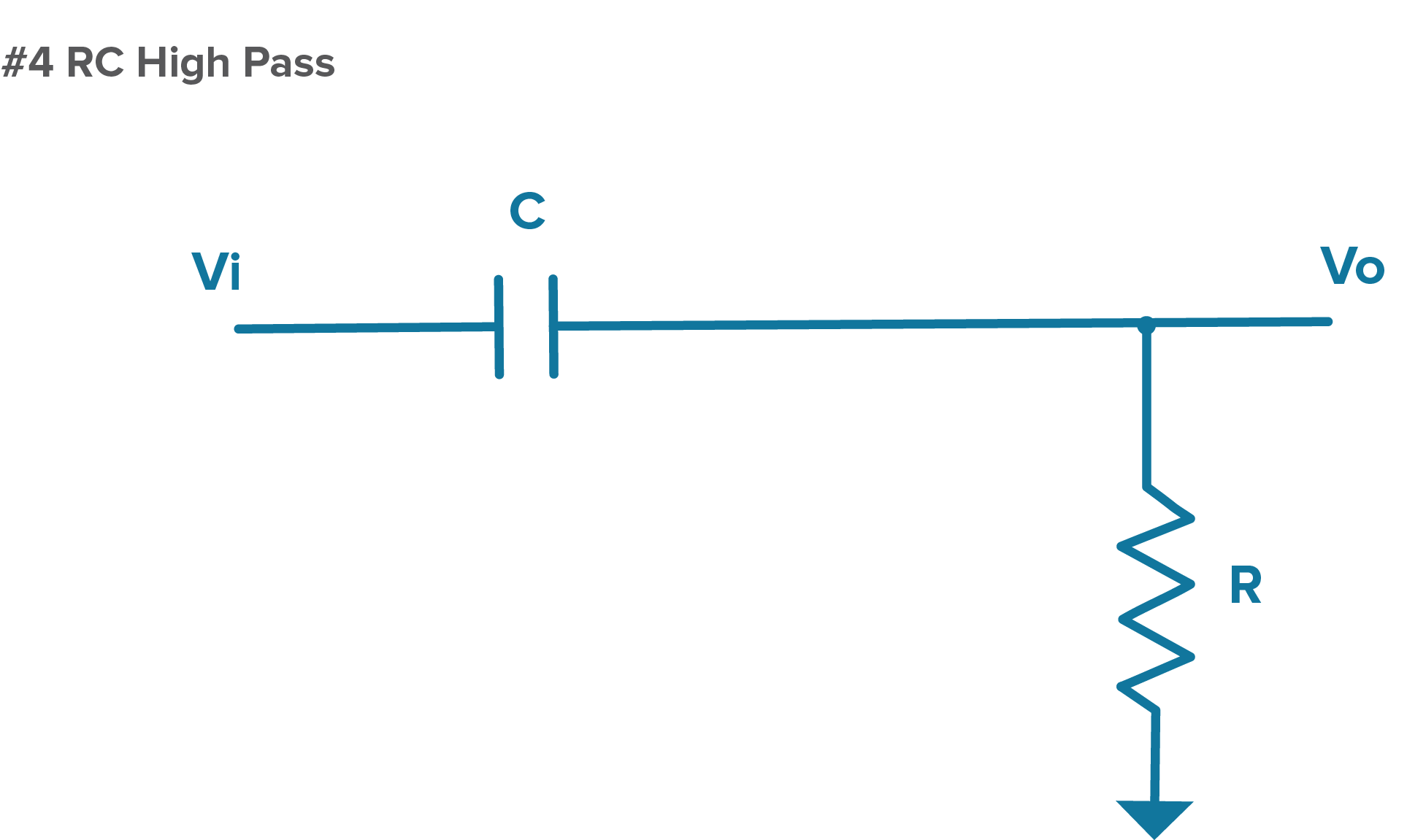
Figure 4. A diagram of an RC high-pass filter.
In this configuration, low frequencies see impedance that is higher than R, so the low-frequency signals go to ground while the high-frequency signals see an impedance lower than R, which means we get a high-frequency output.
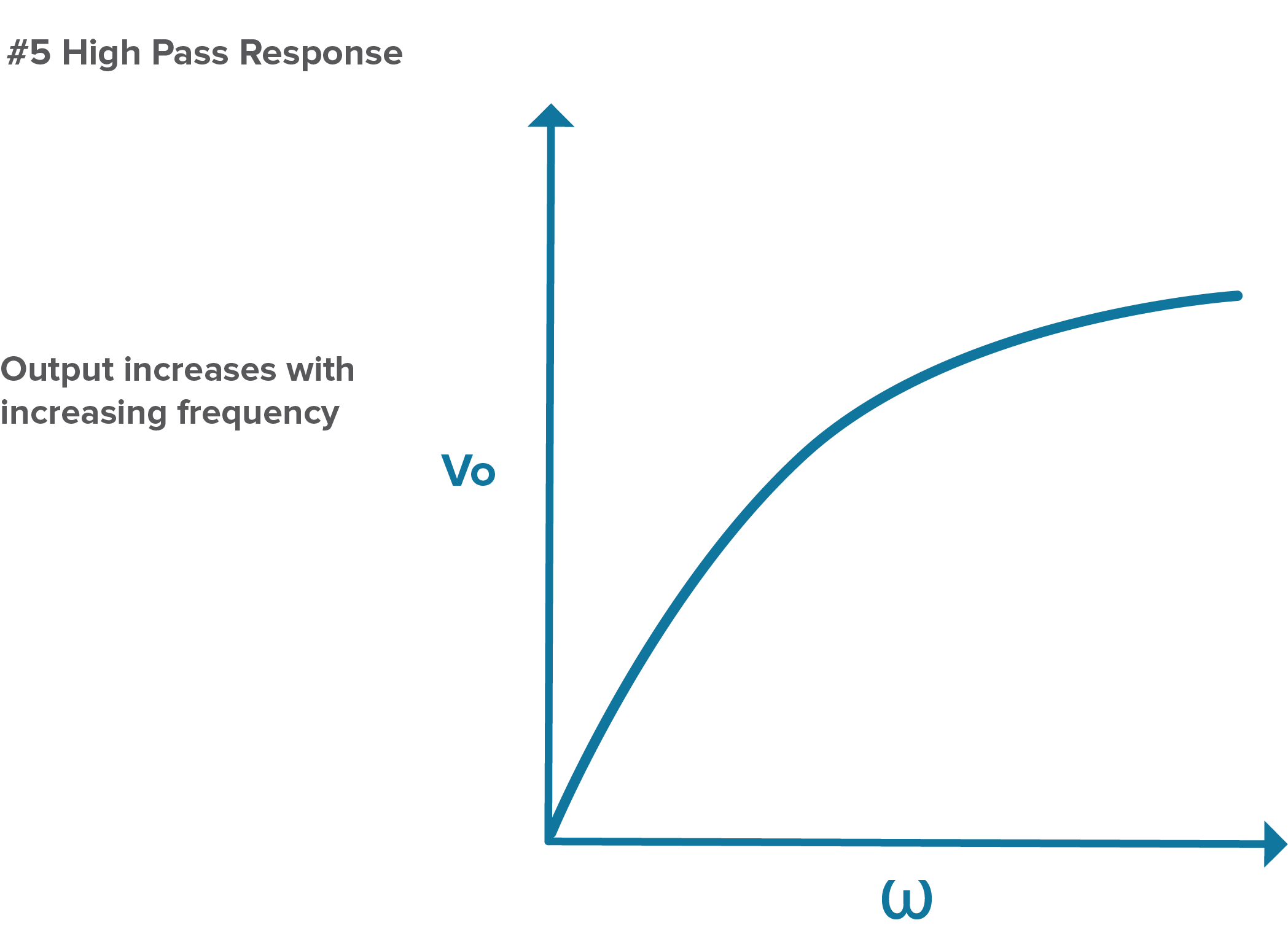
Figure 5. Output voltage increases with increasing frequency when using a high-pass RC filter.
Swapping Cs and Ls to Create Your Desired Filter
Before we jump into talking about how to create different filter configurations by swapping Cs with Ls, let’s recap what we covered in Part 1 on inductors. Inductors have the opposite response to frequency than capacitors. This can be calculated as follows:
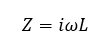
L = Inductance
This means that impedance increases with frequency in an inductor. To create a low-pass filter using an R and L, we can start with an RC high-pass filter as shown in Figure 4 and swap the C for an L. We can also take the same type of approach to design a high-pass filter if we start with a RC low-pass filter as shown in Figure 2 and replace the C with an L. Both examples are illustrated in Figure 6.
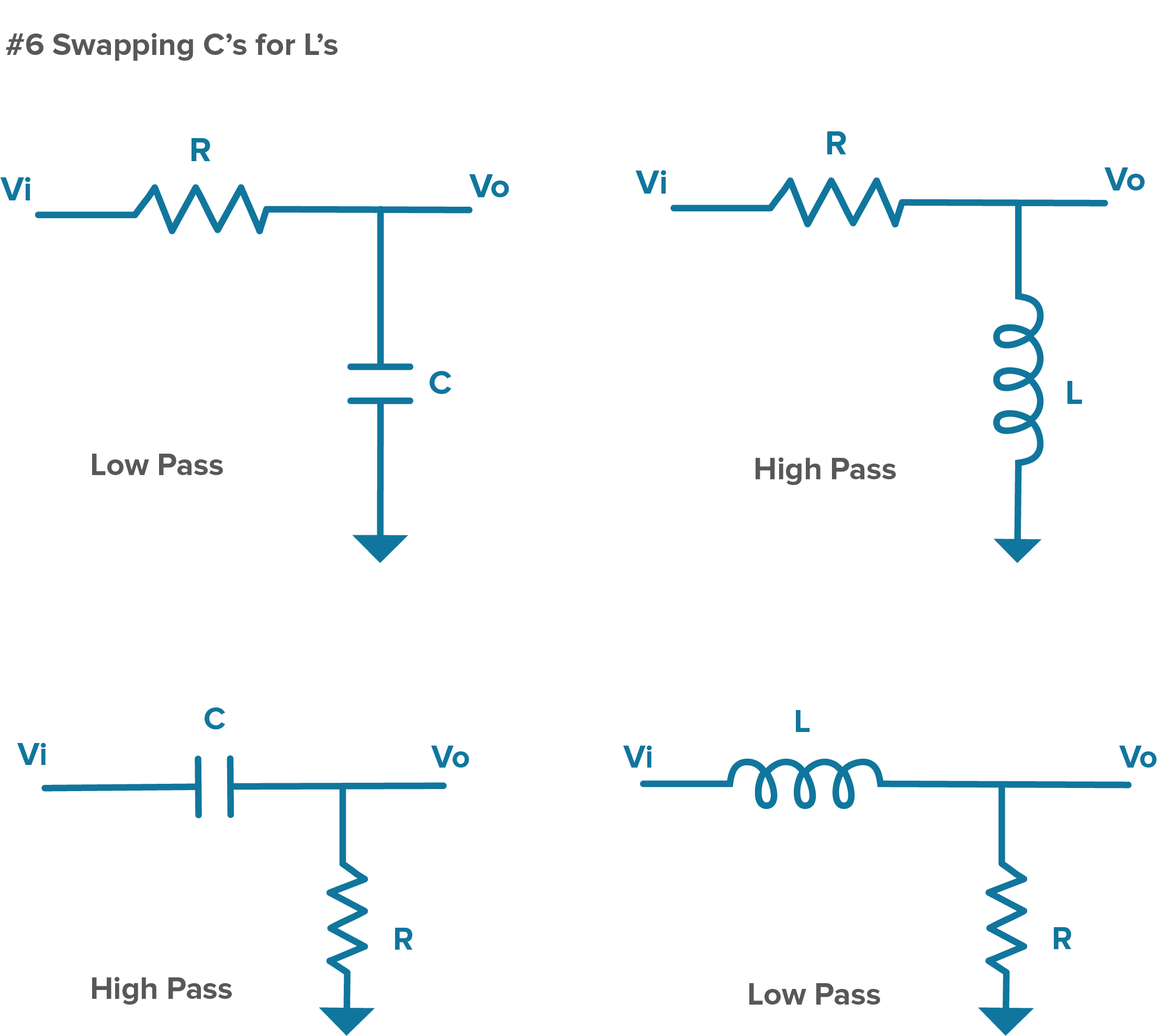
Figure 6. In the top diagram, a low-pass filter is converted to a high-pass filter by swapping the C for an L in the path to ground. In the bottom diagram, the high-pass filter is converted to a low-pass filter by swapping the C for an L in the output line.
As it turns out, RC filters don’t provide the best performance in terms of roll off, which is the slope over frequency from passing a signal to blocking it. To improve this, RF designers can combine Cs and Ls, balancing their opposite responses to frequency to build different low-pass, high-pass, and band pass LC filter responses as shown in Figure 7.
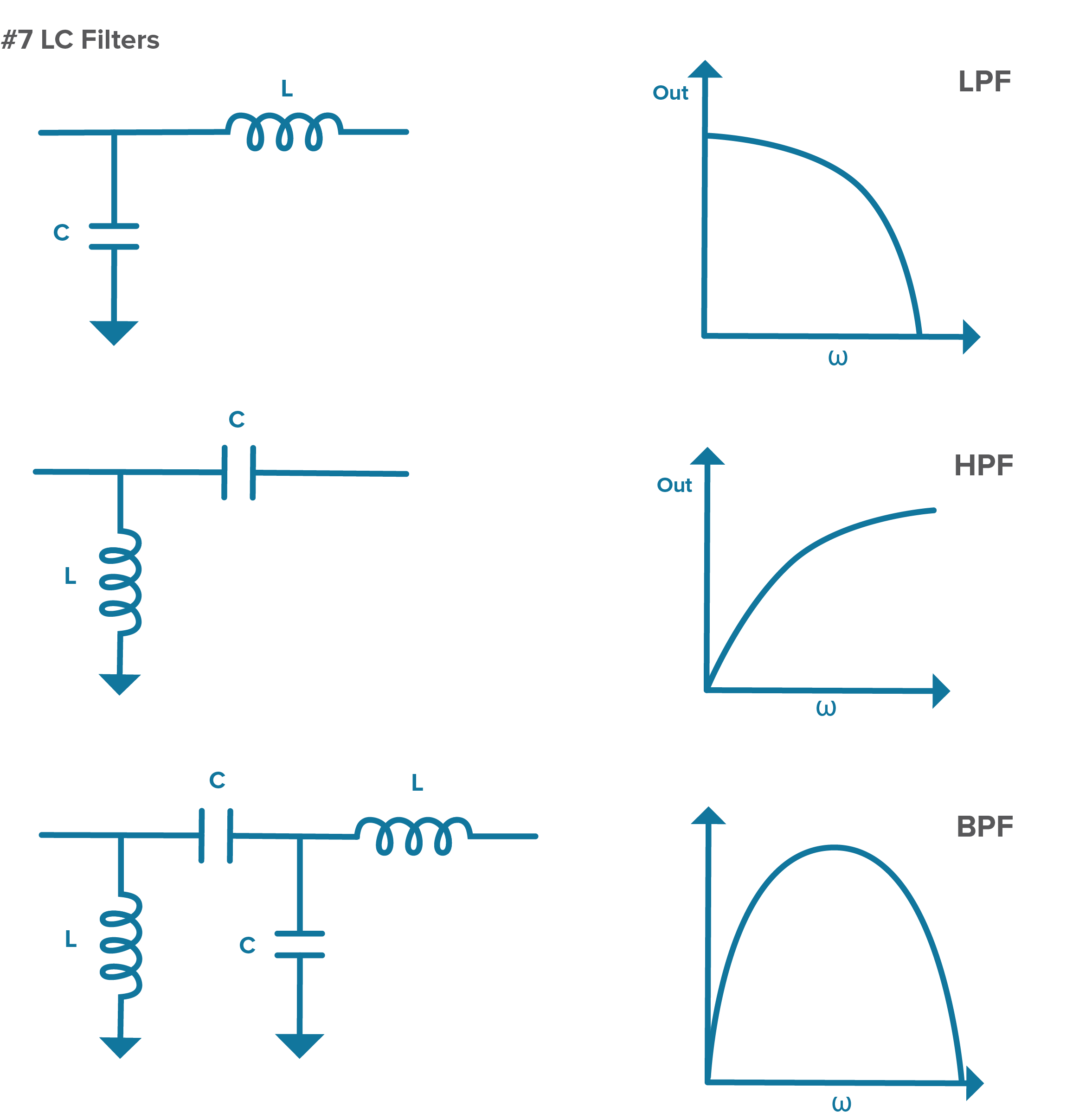
Figure 7. Different types of LC filters and their frequency responses.
Manipulating Impedance to Achieve a Desired Frequency Response in Your Filter
Given that Rs, Cs, and Ls offer different variations on impedance, we can think of designing a filter response as manipulating different impedances to achieve a desired frequency response. Thinking back to the DC voltage divider we started with at the beginning of this post, we can build on this to create a high pass circuit by adding networks of impedance (Zs) using various combinations of RCs and LCs as discussed throughout this post. Figure 8 below shows a high pass circuit where Z1 decreases with frequency and Z2 increases with frequency. In general, by replacing individual Rs, Cs, and Ls with sections of a circuit that have very specific impedance vs frequency behavior, we can create more complex high-performance filters.
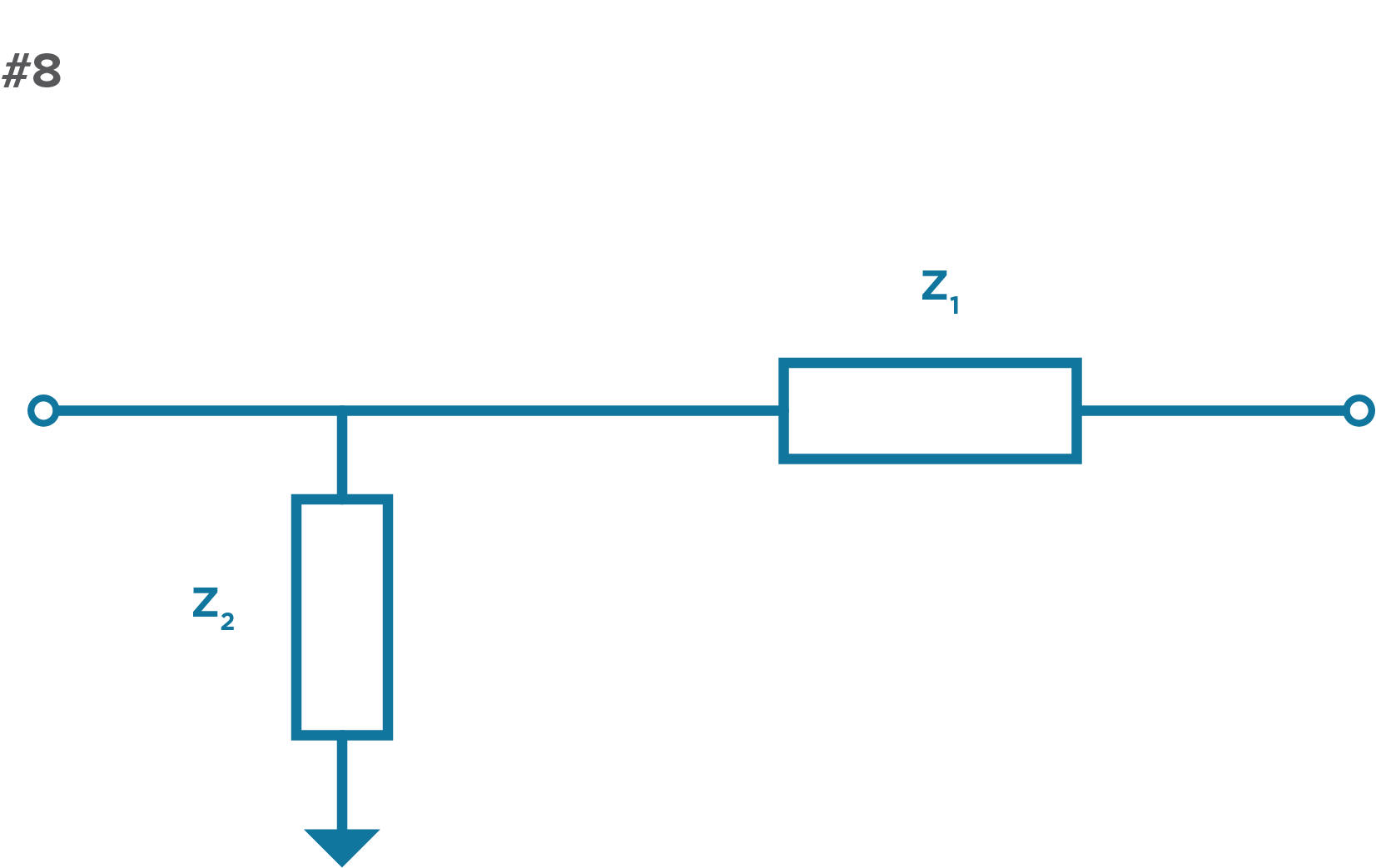
Figure 8. In this example, L and C are replaced with impedances Z1 and Z2.
By breaking down the different ways to use the frequency dependencies of Cs and Ls, you can see how it is possible to get a variety of different filter responses and form simple filters that can serve as the building blocks for more complex filtering needs.
In  , we will take a closer look at what drives various filter responses with an overview of some of the different filter specifications you are likely to encounter out in the wild. In the meantime, visit our
, we will take a closer look at what drives various filter responses with an overview of some of the different filter specifications you are likely to encounter out in the wild. In the meantime, visit our  to checkout additional posts in this multi-part series or take a deeper dive in the fundamentals of RF Filters by downloading the comprehensive Filter Basics guide today.
to checkout additional posts in this multi-part series or take a deeper dive in the fundamentals of RF Filters by downloading the comprehensive Filter Basics guide today.


