When selecting a filter implementation, one factor that is common across all frequencies is optimizing the size of the filter given the application and the required performance. At mmWave frequencies this can be prove to be a particularly interesting problem, given the change in the physical dimensions of the system as one moves from say 600MHz to 38GHz.
Millimeter wave frequencies often refer to the frequency range covering 30GHz to 300GHz, and at those frequencies the wavelengths involved are 10mm to 1mm (take a look at our blog post on An Introduction to the 5G Frequency Spectrum to learn more about the bands being utilized for 5G Fixed Wireless Applications, for example).
The reduction in wavelength brings about some benefits, since the physical size of antennas at mm-wave frequencies become sufficiently small that it makes sense to build complex antenna arrays on chips or the PCB directly.
This is desirable from an overall size reduction standpoint, but antenna arrays are also getting built on a very small scale because of some of the constraints that come with engineering with mm scale wavelengths: In phased array antennas the elements must be sufficiently close together to avoid generating grating lobes – and half wavelength spacing for mmWave frequencies amounts to a few millimeters.
In mmWave applications whether filters are mounted close to each antenna or at some location that feeds the antenna array, considering the size of the filter relative to the rest of the front end becomes important - it becomes physically cumbersome to mount devices close to the antenna that are appreciably different in size to the antenna (or the antenna array) itself.
Filters at mmWave come in all shapes and sizes – we recently took a look at the datasheet dimensions for bandpass filters up at these frequencies of interest to 5G applications. Plotting the area a part occupies (ignoring for the time being the thickness, which tends to scale with the x y dimensions) one arrives at something like this:
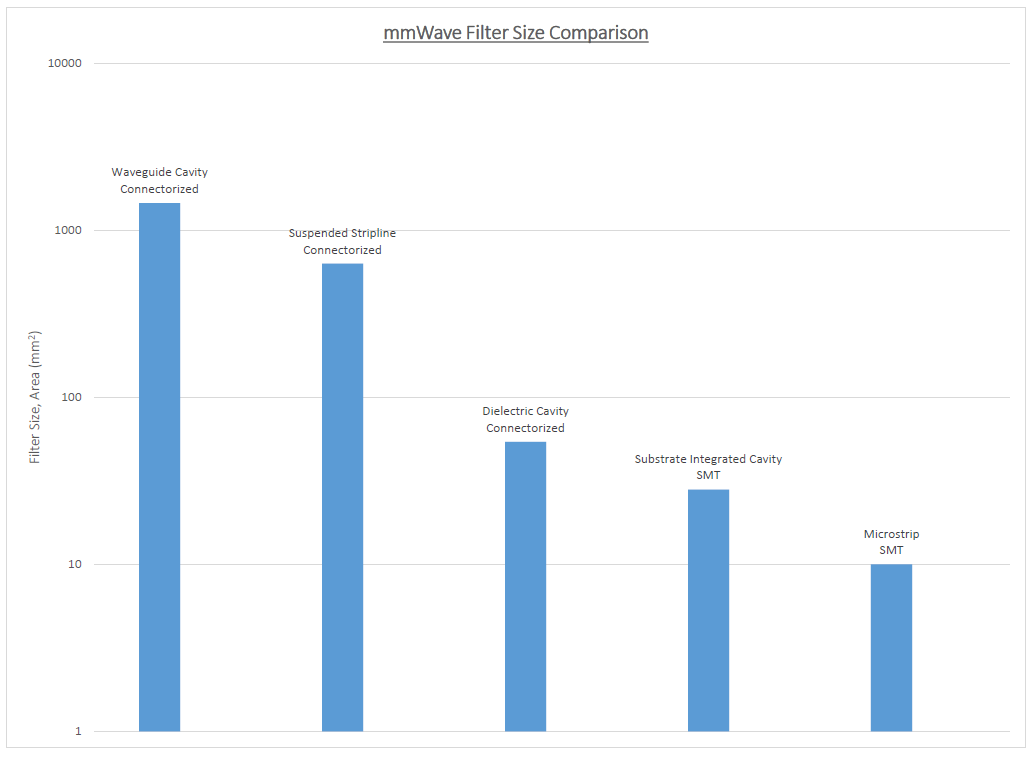
One can see a definite difference between the filters implemented in a connectorized housing and the surface mount implementations. Generally, for radio systems being built on a small scale surface mount approaches are preferred (for more information on 5G system architecture and the need for surface mount components download Reduce Cost and Complexity in 5G mmWave systems with Surface Mount Solderable Filter Components)
Amongst surface mount implementations, the Microstrip approach allows one to reduce the space taken up by a filter in a design while maintaining the levels of performance (in terms of bandwidth, rejection and insertion loss) that cannot be reached by implementing the filter in CMOS for example.
With that said not all Microstrip filters are created equal! Choice of substrate, plating technology and topology can dramatically reduce the size of a surface mount microstrip filter.
Take substrate choice for example. As part of a ‘back of the envelope’ estimate we can look at the wavelength of a signal propagating along microstrip of varying dielectric constants.
Wavelength is related to dielectric constant (relative permittivity) by:
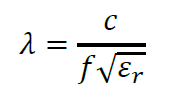
Where c = speed of light, f = frequency and er = dielectric constant.
Now with Microstrip the effective dielectric constant is slightly less than the substrate's dielectric constant, since part of the fields from the microstrip conductor exist in air. But for the sake of this exercise we can overlook that since we are looking to see how wavelength scales with dielectric constant.
Wavelength scales with the inverse of the root of dielectric constant: That is, for a dielectric constant of 25, say, compared to a dielectric constant of 4, a wavelength in the higher dielectric material would be 2.5 smaller than that in the lower dielectric material. Here are some common dielectrics, with PG, CF and CG denoting dielectrics commonly used by Knowles Precision Devices DLI to construct miniature filters:
| Material | Dielectric constant | ~Wavelength at 25GHz (mm) |
| PTFE | 2.1 | 8.3 |
| FR-4 | 4.8 | 5.5 |
| Alumina, 99.6% | 9.9 | 3.8 |
| PG | 12.5 | 3.4 |
| CF | 25 | 2.4 |
| CG | 67 | 1.5 |
Classical Bandpass Filter Topologies can be grouped into those where the resonators are formed by a) half wavelength long open circuit lines and b) quarter wavelength long short circuit lines, so given the same topology the physical size of the filter can be dramatically impacted by the choice of substrate.
High dielectric constant, Hi-Q materials offer reduced size versus on PCB: With careful topology choice, up to 20x using CG material, 10x using CF, and 3 times using PG versus typical PCB.
To learn more about Microstrip filter technology download our white paper Microstrip Filter Topologies or visit our Microwave Products Page.

