Spectral efficiency, or bandwidth efficiency, tells us about the channel capacity over a 1Hz bandwidth. It is a measure of the efficiency of a physical layer protocol when it comes to utilizing the spectrum available. To understand how spectral efficiency is calculated, it’s first important to understand the Shannon-Hartley Theorem in the context of 5G mmWave applications (which we discussed in an earlier blog post).
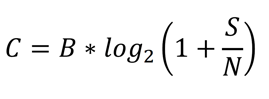
Where:
C= Channel Capacity in bits/second
B = Bandwidth in hertz
S = transmit power, in Watts
N = noise on channel, in Watts
S/N = Signal to noise ratio
Now from this it is possible to ask: How many bits/second can we expect get for each chunk of Bandwidth?
The Shannon-Hartley bound says that the error free bit rate (Rb) must be less than the channel capacity:
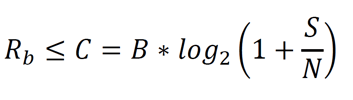
We can divide our bit rate Rb by the bandwidth B to get a definition of the bounds of Spectral Efficiency:
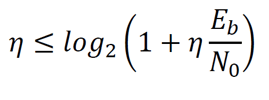
Where:
η = Spectral Efficiency, Rb/B, in bits per second per Hertz
Eb/N0 = The ratio of energy per bit to noise power spectral density ratio, or normalized signal to noise ratio, where:
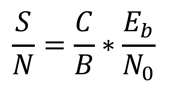
If you are just getting started with the concept of spectral efficiency, Wikipedia currently has a nice summary table of the Spectral efficiencies of common communication systems that is interesting to look at for historical context. 1G cellular, for example, exhibited a spectral efficiency of 0.45 bps/Hz, circa 1981 whereas LTE-Advanced (2013) can reach 30 bps/Hz with 8x8 MIMO. And, 5G is looking to make even more dramatic advances in the realm of spectral efficiency. In 2016 for example a team at the University of Bristol set a rate of 145.6 bps/Hz below 6GHz and a Nokia Bell Labs team reported an efficiency of 100bps/Hz at 28GHz.
At 500MHz bandwidth 100bps/Hz represents a data rate of 50Gbps, suggesting that the stated goal for 5G of 20Gbps is well within reach for mmWave systems. It should be noted though that not all of the 500MHz would be available for data – there are things like system overhead to take into account as well as system bandwidth tolerances that would eat away at this blazing 50Gbps. It is important to note that high spectral efficiency comes from innovative use of tools like modulation schemes and MIMO.
This leads to an interesting question about how we should specify RF filters for such systems. Given that spectral efficiencies continue to increase, an incredible amount of data will be packed into a humble 1Hz bandwidth and perhaps even up at mmWave frequencies, where bandwidth seems to be plentiful, the hard-fought gains brought about by such advances in spectral efficiency should not be squandered by wasting bandwidth. We should begin to think about how much bandwidth we can tolerate losing to temperature variation, for example, if each MHz in bandwidth carries with it 100 Mbps.
At Knowles Precision Devices, we have looked closely at microstrip filter temperature stability and one key variable is the substrate material. Take for example this comparison between two 18GHz band-pass filter designs, one lot manufactured on our ‘CF’ substrate and the other on an Alumina board. We measured the filter response from -55°C to +125°C:
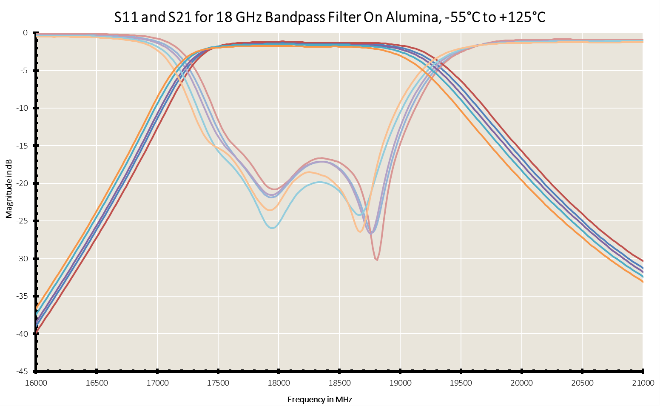
Figure 1 .Response of Microstrip Bandpass Filters on Alumina
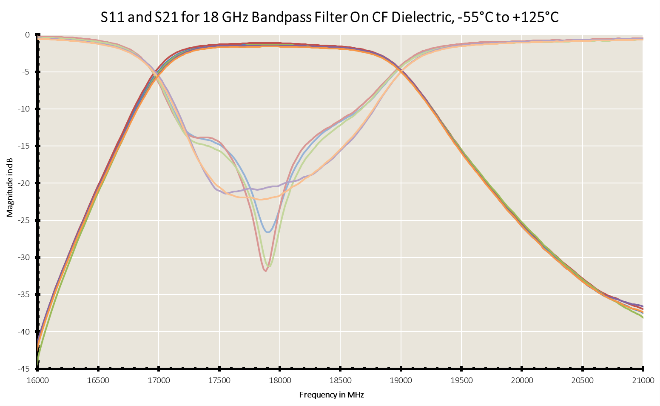
Figure 2. Response of Microstrip Bandpass Filters on CF Dielectric
On the high side of the Alumina based filter we saw a 300MHz shift and on the low side a shift of 140MHz. At spectral efficiencies in the range of 100bps/Hz a shift in bandwidth of the order of just 10MHz could equate to 1Gbps of channel capacity, something that the data-rate focused world of 5G may find hard to tolerate.
Dealing with such high spectral efficiencies up in the mmWave range brings with it new concerns about the way in which an RF system's bandwidth responds to changes in temperature, for example. Talk to an RF filter design expert at Knowles Precision Devices to ensure the substrate technology used to implement your filter structures is right for your application.
Additional resources are available to learn more about Knowles Precision Devices DLI brand 5G solutions and our mmWave filters and microstrip technology.

